Maxによるロジスティック写像 〜漸化式をMaxで実装〜

ロジスティック写像という方程式をご存知でしょうか？離散的な変数nを持つ量xを以下の差分方程式で与えた時の現象のことです．

\[x_n=ax_{n-1}(1-x_{n-1})\]

aは定数です．例えば，

\[a=2\]

として

\[x_0=0.001\]

から計算を始めると，

\[x_1=2\times0.001\times(1-0.001)=0.001998\]
\[x_2=2\times0.001998\times(1-0.00998)=0.31975992\]
\[x_3=2\times0.31975992\times(1-0.31975992)=0.5329816\]
\[x_4=2\times0.5329816\times(1-0.5329816)=0.49691391\]
\[x_5=2\times0.49691391\times(1-0.49691391)=0.49998095\]
\[x_6=2\times0.49998095\times(1-0.49998095)=0.5\]
\[x_7=2\times0.5\times(1-0.5)=0.5\]

・・・

というようにxは0.5に収束します．（この式では，一度0.5になってしまえば，もうそれ以上変化のしようがないことがわかります．）

このことを図にするとこのようになります．

（やってみればわかりますが）初期値が0.001以外でも，xは0.5に収束します．しかし，これはa=2の場合の話です．aを他の値にしたときの様子も見てみましょう．

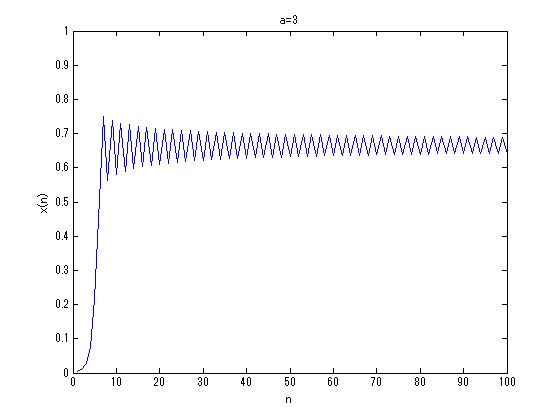
a=3のとき，xは2つの値を繰り返す変化に収束するようです．

ちょっと見づらいですが，a=3.5のとき，4つの値を繰り返します．

aの値が増えると，徐々にxの変化の乱雑さが増えていきます．

a=4になると，ほとんど法則性なく変化しているといってもいいような変化をするようになります．しかし，この変化も冒頭で紹介したロジスティック写像の式の計算結果です．aの値が違うだけで実に多種多様な変化をもたらす方程式だということが分かります．このことを表したのが，有名な図

です．横軸がaの値．aの値によってxがどんな値に収束するかを表しています．ロジスティック写像の驚くべき点は，決定論的な法則による変化であるはずなのに，そうとは思えない変化をもたらすことです．このように，決定論的な法則があるにもかかわらず，見た目にはその法則が見出せないような変化をする系のことを「カオス力学系」と呼びます．ロジスティック写像はカオス力学系の非常に初歩的な例の一つです．

MATLABでロジスティック写像を実装してみます．aの値を変化させながらxの値をプロットしていきます．

clear;
close all;
len=100000;
starta=2.9;
x=zeros(1,len);
a=zeros(1,len);
xmem=0.0000001;
for k=1:len,
    a(k)=(4-starta)*k/len;
    a(k)=a(k)+starta;
    x(k)=a(k)*xmem*(1-xmem);
    xmem=x(k);
end
figure(2);
plot(a,x,'.','MarkerSize',1);
xlim([starta,4]);
ylim([0,1]);

実装のポイントは，「前回のxの値」を保持しておいて，それを「現在のxの値」の算出に利用するところです．

実行結果はこのようになります．

先ほどの図に比べて分岐のところで非連続な感じになっているのは，aを変化させる刻み幅が広いからです．

こうした，現在の値が過去の値によって決定されるような関係式のことを「漸化式」と呼びます．こうした漸化式は，コンピュータプログラミングで実装するのが簡単なので，コンピュータサイエンスが発展すると盛んに研究されるようになりました．一般にコンピュータによる数値計算は，いかに問題を漸化式に落とし込むかということが重要になるといっても過言ではありません．（オイラー法なんかがまさに良い例です．）

MATLABのようなソースコードを書いていくプログラミグ環境で漸化式を実装するのは非常に簡単です．一方，Maxのようなビジュアルプログラミング環境で行うにはどうしたらいいでしょうか？結論から言うと，Maxでロジスティック写像を実装するにはこのようになります．

このパッチで重要なのはf（floatの略）オブジェクトです．fは第二インレットに入った浮動小数点数を保持して，第一インレットにbangが入った時に保持した値をアウトレットから出力します．その値を使って，その下にある部分でロジスティック写像の計算を行います．この時，t（triggerの略）オブジェクトとRight to Left Orderを利用して，計算の順番を冒頭の式の通りに制御している点にも注目したいところです．そして，計算結果をまたfloatに入れてまで保持します．保持した値が次のbangの入力によって出力され，再びロジスティック写像の計算を行います．これをbangの入力の度に繰り返します．
ここで意識したいのは，一度fオブジェクトにbangが入力されると，ロジスティック写像の計算をして，もう一度fオブジェクトに計算結果を格納するまでが，ひとかたまりの処理として行われるということです．このひとかたまりの処理は原則同期的に行われるので，処理をし終わるまでパッチは他の処理を行いません．（非同期に動作するオブジェクトは別です．）

このように，Maxのプログラミング環境としての特徴を意識すれば，少し込み入った制御構造もパッチのみで実装することができます．